
In simple words, quartiles are values that divide a data set into quarters after the data set has been ordered each quartile has a name and they are: Q 1, Q 2 Q_1, Q_2 Q 1 , Q 2 and Q 3 Q_3 Q 3 . Just as its name indicates, a quartile focuses on dividing the data distribution into four parts, where each quartile is the specific point marking the division between the first quarter and the second, the second quarter and the third or the third quarter and the fourth.
Therefore, there are 7 data values in the set before Billys score, which means Billy got a 83% in his Biology course. Interquartile Range & Box-and-Whisker Plotįor the data set: = 7 100 70 × 10 = 7 Equation 6: Finding Billys score.Relative to their respective mean and standard deviation, who got the better grade? Using Z-score to Compare the Variation in Different PopulationsĬharlie got a mark of 85 on a math test which had a mean of 75 and a standard deviation of 5.ĭaisy got a mark of 75 on an English test which had a mean of 69 and a standard deviation of 2.Included are a variety of tests of significance, plus correlation, effect size and confidence interval calculators.
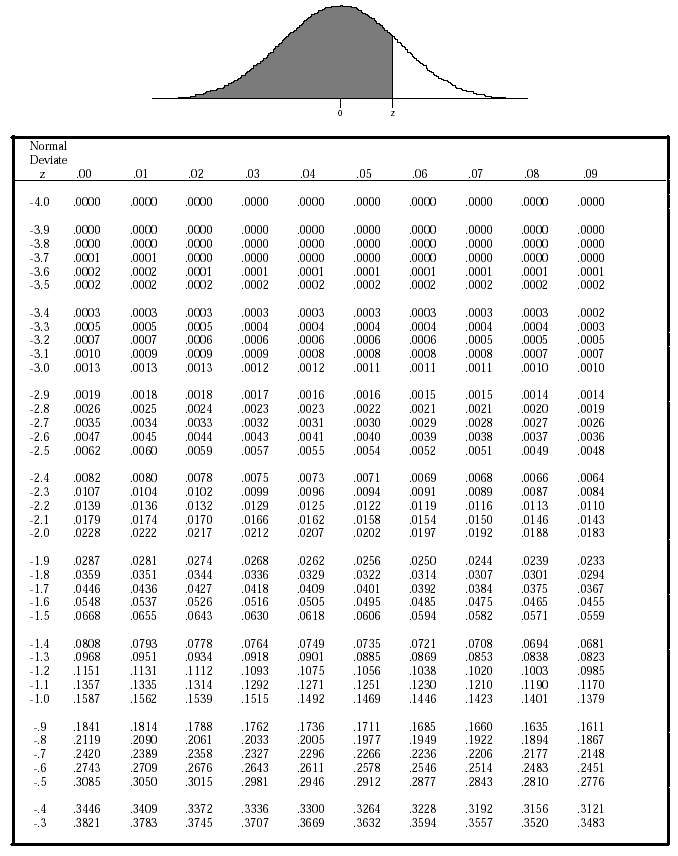
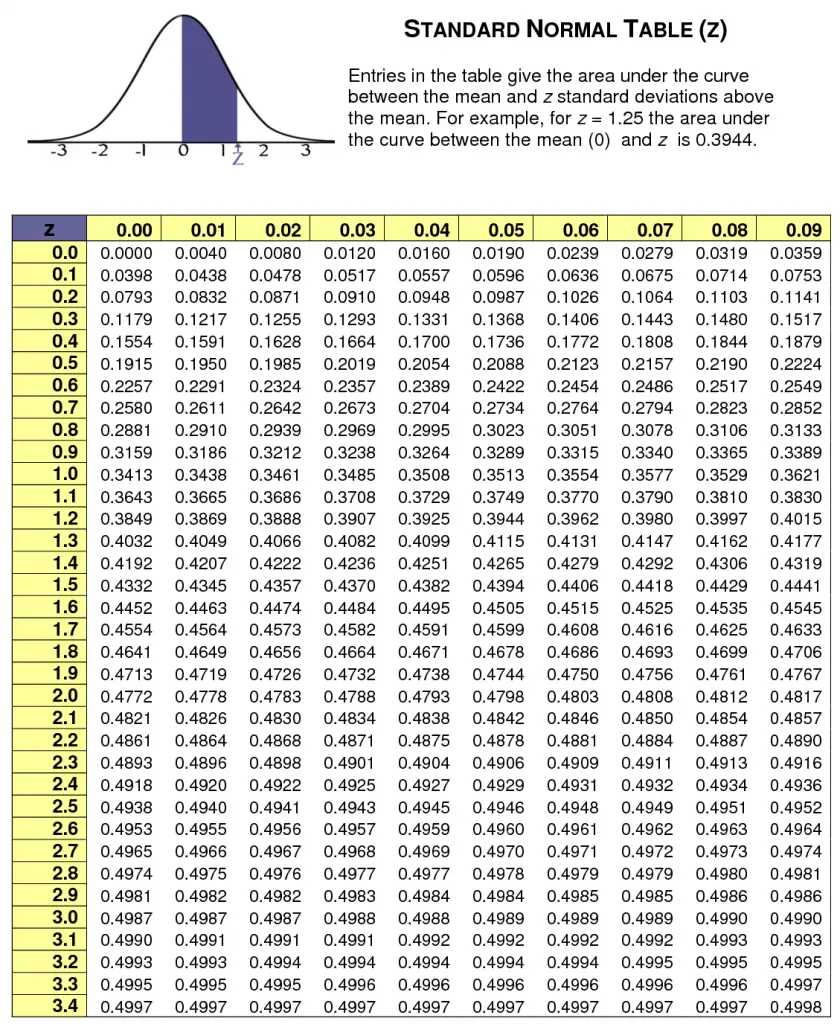
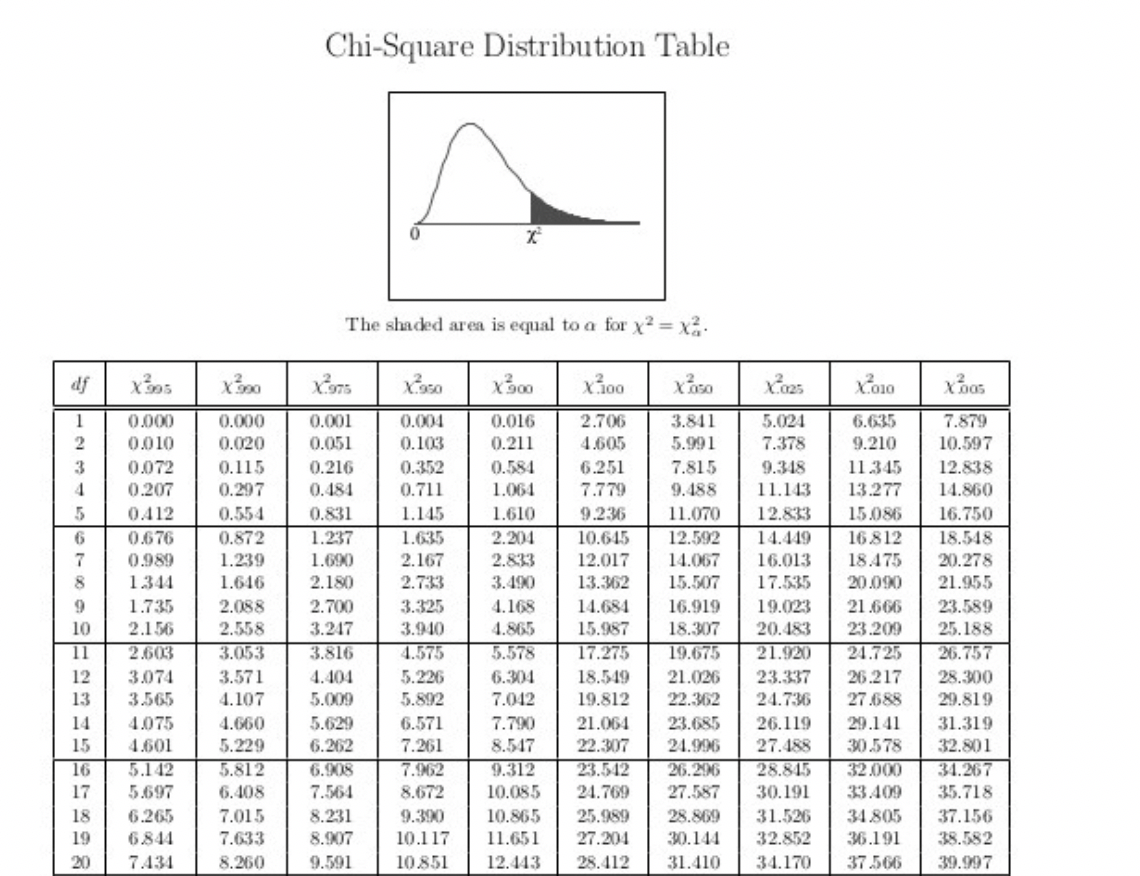
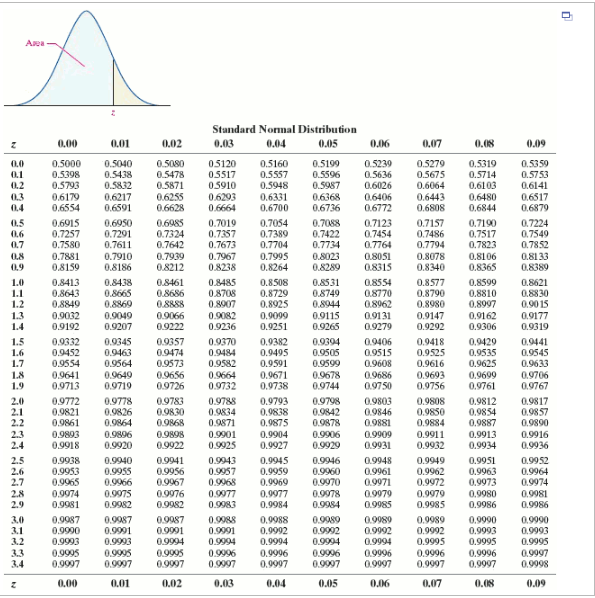
Percentile (between 0 and 1) Z-Score: -0.6745 Published by Zach View all posts by Zach Prev Left Skewed vs. Simply enter a percentile in the box below and then click the Calculate button. This value indicates that 74.857 of all apple weights will be lower than our apple weight of 110 grams. Januby Zach Percentile to Z-Score Calculator This calculator finds the z-score associated with a given percentile. This equates to the area of the distribution below Z. Cumulative gives a probability that a statistic is less than Z. The truncated z-table below shows the area for our z-score. Here you'll find a set of statistics calculators that are intuitive and easy to use. The z-score for our apple is (110-100) / 15 0.67. For example, here is how to convert a percentile of 0.85 to a z-score: It turns out that a percentile of 0.85 corresponds to a z-score of roughly 1.036.


 0 kommentar(er)
0 kommentar(er)
